Although matrices are not first-class citizens in Power Query, a business problem often comes along, which might greatly be simplified by thinking of it in matrix terms.
You can, of course, imitate matrices in Power BI through tables, two-dimensional lists or records, but this approach doesn’t come with any matrix related functions. So as always, you have to roll up your sleeves and roll out your own set of needed operations.
I want to share an approach of doing matrix multiplication which can be translated into other algebra operations.
We’ll start by reviewing how matrix multiplication works from the diagram below.
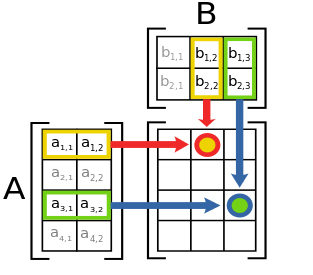
If we break down the problem, we can think of two matrices A and B, in M(Power Query) terms as two tables with matching size of rows in matrix A and columns in matrix B, respectively. Then the matrix multiplication operation can be reduced to a problem of iterating through all row and column combinations and computing the dot product of equally sized vectors.
The dot product in M can be performed by using List.Accumulate, which aggregates the product of a List.Zip, pulls the respective elements of two vectors into tuples. Here is the code.
dotProduct = (v1,v2) =>
List.Accumulate(
List.Zip({v1,v2}),0,(agg,_)=> agg+(_{1}*_{0}))
Next, we breakdown the matrix A into rows – Table.ToRows(A) – and matrix B into columns Table.ToColumns(B). And iterate through all the combinations of row vectors and column vectors to accumulate the results into a nested list of dot products.
Check the code below for the use of nested List.Accumulate.
List.Accumulate(Table.ToRows(A),
{},
(_,ai)=> _&{ List.Accumulate(Table.ToColumns(B),
{},(_,bj)=> _&{ dotProduct(ai,bj) })
})
Putting the two operations together results in the following final function:
| (A,B) => | |
| let | |
| //vector multiplication | |
| dotProduct = (v1,v2) => | |
| List.Accumulate( | |
| List.Zip({v1,v2}), | |
| 0, | |
| (agg,_)=> | |
| agg+(_{1}*_{0})) | |
| in | |
| Table.FromRows( | |
| List.Accumulate(Table.ToRows(A), | |
| {}, | |
| (_,ai)=> | |
| _& { List.Accumulate(Table.ToColumns(B), | |
| {}, | |
| (_,bj)=> | |
| _&{ dotProduct(ai,bj) }) | |
| }) | |
| ) |


This is a real great article . IS it possible to do the exact same thing with measure instead ? I would need to implement the dotProduct but using measure instead . cause at the end what i d like to do is to calculate Cosine similarity between 2 documents that are represented by vectors of words
LikeLike
This is a real great article . IS it possible to do the exact same thing with measure instead ? I would need to implement the dotProduct but using measure instead . cause at the end what i d like to do is to calculate Cosine similarity between 2 documents that are represented by vectors of words
LikeLike